A competição
Para quem ainda não conhece o site Kaggle contém vários desafios onde os participantes buscam soluções para diversos problemas envolvendo aprendizado de máquina (machine learning). Um desafio não muito novo, mas bastante popupar é o do Titanic.
Neste desafio é preciso prever quais pessoas vão sobreviver ou não com base em dados reais do naufrágio.
import numpy as np
import pandas as pd
import matplotlib as mpl
import matplotlib.pyplot as plt
import matplotlib.pylab as pylab
import seaborn as sns
%matplotlib inline
#Cria as funções para mostrar os gráficos
#Source https://www.kaggle.com/sachinkulkarni/titanic/an-interactive-data-science-tutorial
def plot_correlation_map( df ):
corr = titanic.corr()
_ , ax = plt.subplots( figsize =( 12 , 10 ) )
cmap = sns.diverging_palette( 220 , 10 , as_cmap = True )
_ = sns.heatmap(
corr,
cmap = cmap,
square=True,
cbar_kws={ 'shrink' : .9 },
ax=ax,
annot = True,
annot_kws = { 'fontsize' : 12 }
)
def plot_line(loss, ylabel, xlabel='Epochs'):
fig = plt.figure()
plt.plot(loss)
plt.ylabel(ylabel)
plt.xlabel(xlabel)
plt.show()
plt.show()
def plot_histograms( df , variables , n_rows , n_cols ):
fig = plt.figure( figsize = ( 16 , 12 ) )
for i, var_name in enumerate( variables ):
ax=fig.add_subplot( n_rows , n_cols , i+1 )
df[ var_name ].hist( bins=10 , ax=ax )
ax.set_title( 'Skew: ' + str( round( float( df[ var_name ].skew() ) , ) ) ) # + ' ' + var_name ) #var_name+" Distribution")
ax.set_xticklabels( [] , visible=False )
ax.set_yticklabels( [] , visible=False )
fig.tight_layout() # Improves appearance a bit.
plt.show()
def plot_distribution( df , var , target , **kwargs ):
row = kwargs.get( 'row' , None )
col = kwargs.get( 'col' , None )
facet = sns.FacetGrid( df , hue=target , aspect=4 , row = row , col = col )
facet.map( sns.kdeplot , var , shade= True )
facet.set( xlim=( 0 , df[ var ].max() ) )
facet.add_legend()
def plot_categories( df , cat , target , **kwargs ):
row = kwargs.get( 'row' , None )
col = kwargs.get( 'col' , None )
facet = sns.FacetGrid( df , row = row , col = col )
facet.map( sns.barplot , cat , target )
facet.add_legend()
Lendo os dados
Para o desafio do titanic são disponibilizados 2 arquivos. Um de treino e outro de teste. Para que a normalização dos dados possa ser feita, ambos são concatenados em um único DataFrame (full).
| Variable | Definition | Key |
|---|---|---|
| survival | Survival | 0 = No, 1 = Yes |
| pclass | Ticket class | 1 = 1st, 2 = 2nd, 3 = 3rd |
| sex | Sex | |
| Age | Age in years | |
| sibsp | # of siblings / spouses aboard the Titanic | |
| parch | # of parents / children aboard the Titanic | |
| ticket | Ticket number | |
| fare | Passenger fare | |
| cabin | Cabin number | |
| embarked | Port of Embarkation | C = Cherbourg, Q = Queenstown, S = Southampton |
train = pd.read_csv("train.csv")
test = pd.read_csv("test.csv")
full = train.append( test , ignore_index = True )
titanic = full[ :891 ]
titanic.head()
| Age | Cabin | Embarked | Fare | Name | Parch | PassengerId | Pclass | Sex | SibSp | Survived | Ticket | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 22.0 | NaN | S | 7.2500 | Braund, Mr. Owen Harris | 0 | 1 | 3 | male | 1 | 0.0 | A/5 21171 |
| 1 | 38.0 | C85 | C | 71.2833 | Cumings, Mrs. John Bradley (Florence Briggs Th... | 0 | 2 | 1 | female | 1 | 1.0 | PC 17599 |
| 2 | 26.0 | NaN | S | 7.9250 | Heikkinen, Miss. Laina | 0 | 3 | 3 | female | 0 | 1.0 | STON/O2. 3101282 |
| 3 | 35.0 | C123 | S | 53.1000 | Futrelle, Mrs. Jacques Heath (Lily May Peel) | 0 | 4 | 1 | female | 1 | 1.0 | 113803 |
| 4 | 35.0 | NaN | S | 8.0500 | Allen, Mr. William Henry | 0 | 5 | 3 | male | 0 | 0.0 | 373450 |
titanic.describe()
| Age | Fare | Parch | PassengerId | Pclass | SibSp | Survived | |
|---|---|---|---|---|---|---|---|
| count | 714.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 | 891.000000 |
| mean | 29.699118 | 32.204208 | 0.381594 | 446.000000 | 2.308642 | 0.523008 | 0.383838 |
| std | 14.526497 | 49.693429 | 0.806057 | 257.353842 | 0.836071 | 1.102743 | 0.486592 |
| min | 0.420000 | 0.000000 | 0.000000 | 1.000000 | 1.000000 | 0.000000 | 0.000000 |
| 25% | 20.125000 | 7.910400 | 0.000000 | 223.500000 | 2.000000 | 0.000000 | 0.000000 |
| 50% | 28.000000 | 14.454200 | 0.000000 | 446.000000 | 3.000000 | 0.000000 | 0.000000 |
| 75% | 38.000000 | 31.000000 | 0.000000 | 668.500000 | 3.000000 | 1.000000 | 1.000000 |
| max | 80.000000 | 512.329200 | 6.000000 | 891.000000 | 3.000000 | 8.000000 | 1.000000 |
Mostrando o início dos dados em formato de tabela com o comando head() é possível observar quais os tipos de dados e que existem alguns valores faltando (Ex: Cabin).
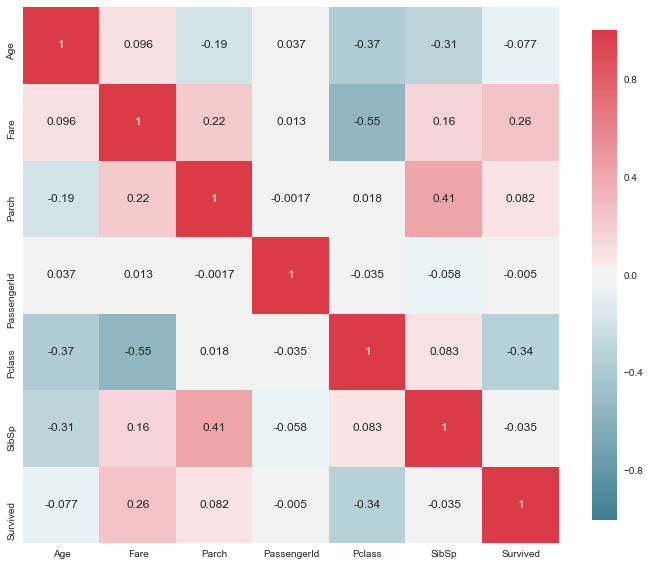
Calcula a correlação de pares.
- Mediana (means)
- Desvio padrão (standard deviation - std)
- Standard Error of the mean: s.std() / np.sqrt(len(s))
Com a correlação de pares é possível ter uma ideia de como uma variável influencia outra, isto é, se existe alguma relação de dependência entre elas.
#print(titanic.mean())
#print(titanic.std())
#print(titanic.sem())
plot_correlation_map(titanic)
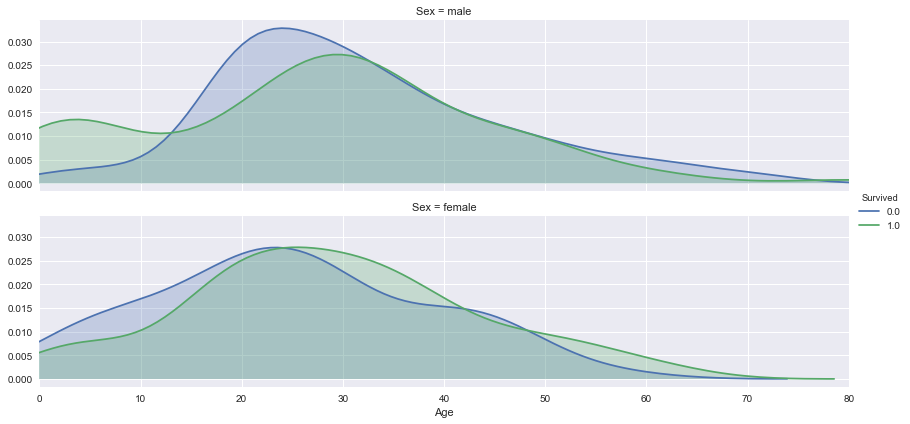
Distribuição
Os gráficos de distribuição possibilitam observar a relação entre duas variáveis. No exemplo abaixo é possível observar que mais homens entre 0 e 10 anos e mulheres entre 30 e 40 anos sobreviveram.
plot_distribution( titanic , var = 'Age' , target = 'Survived' , row = 'Sex' )
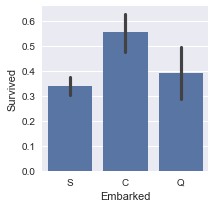
Mostrando um gráfico de barras entre variáveis discretas possibilita avaliar não somente a quantidade, mas também a variação entre a relação de duas variáveis. No exemplo abaixo é possível observar que o local de embarque dos passageiros não influenciou muito no fato de terem sobrevivido ou não.
plot_categories( titanic , cat = 'Embarked' , target = 'Survived' )
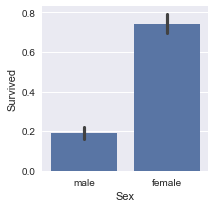
Já o sexo influenciou, onde muito mais mulheres sobreviveram do que homens.
plot_categories( titanic , cat = 'Sex' , target = 'Survived' )
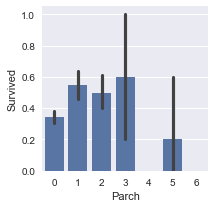
É possível oberver que a classe dos participantes também teve um fator predominante para a sobrevivência
plot_categories( titanic , cat = 'Pclass' , target = 'Survived' )
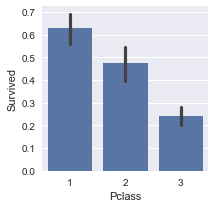
plot_categories( titanic , cat = 'SibSp' , target = 'Survived' )
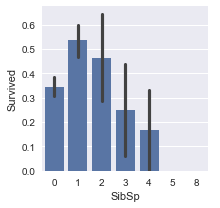
plot_categories( titanic , cat = 'Parch' , target = 'Survived' )
Preparando os dados
Nesta etapa os dados são convertidos e dados faltantes são preenchidos ou eliminados.
No dataset original o sexo dos passageiros está informado com duas palavras (male para homem e female para mulheres). Para podermos usar essa informação em classificadores é necessário convertê-la para um valor numérico. Neste caso, podemos expressar o sexo por meio dos valores 1 (homem) e 0 (mulheres).
sex = pd.Series( np.where( full.Sex == 'male' , 1 , 0 ) , name = 'Sex' )
Outro procedimento comum em data cleaning é a criação de novas colunas com valores 0 e 1s para valores únicos em uma coluna. Abaixo são criadas novas colunas para cada valor únivo de local de embarque e os dados são atualizados para 0 e 1 correspondente ao local de embarque do passageiro.
embarked = pd.get_dummies( full.Embarked , prefix='Embarked' )
embarked.head()
| Embarked_C | Embarked_Q | Embarked_S | |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 |
| 4 | 0 | 0 | 1 |
De forma semalhante, são criadas colunas para cada um dos valores únicos do tipo de classe de passageiros.
pclass = pd.get_dummies( full.Pclass , prefix='Pclass' )
pclass.head()
| Pclass_1 | Pclass_2 | Pclass_3 | |
|---|---|---|---|
| 0 | 0 | 0 | 1 |
| 1 | 1 | 0 | 0 |
| 2 | 0 | 0 | 1 |
| 3 | 1 | 0 | 0 |
| 4 | 0 | 0 | 1 |
Para extrairmos informações de um dataset é necessário que este esteja com todos os valores preenchidos. Caso o dataset tenha algum dado faltanto é possível realizar algumas estratégias:
- Preencher os dados faltantes com a mediana dos valores existentes
- Remover todos os dados dos exemplos faltantes do dataset
Abaixo os valores são preenchidos utilizando a mediana. Dessa forma a distribuição dos dados não é afetada, não influenciando nos resultados dos classificadores (na maioria das vezes).
imputed = pd.DataFrame()
imputed[ 'Age' ] = full.Age.fillna( full.Age.mean() )
imputed[ 'Fare' ] = full.Fare.fillna( full.Fare.mean() )
#imputed['SibSp'] = full.SibSp.fillna( full.SibSp.mean() )
#imputed['Parch'] = full.Parch.fillna( full.Parch.mean() )
imputed.head()
| Age | Fare | |
|---|---|---|
| 0 | 22.0 | 7.2500 |
| 1 | 38.0 | 71.2833 |
| 2 | 26.0 | 7.9250 |
| 3 | 35.0 | 53.1000 |
| 4 | 35.0 | 8.0500 |
Quando a variável faltante não é numérica é possível criar uma nova variável representando os dados faltantes. Abaixo todas as cabines com dados faltantes passam a ter o valor U. Em seguida são criadas e populadas colunas correspondentes a cada cabine.
cabin = pd.DataFrame()
#Substitui os dados de cabines faltantes com U (Unknown)
cabin[ 'Cabin' ] = full.Cabin.fillna( 'U' )
# mapping each Cabin value with the cabin letter
cabin[ 'Cabin' ] = cabin[ 'Cabin' ].map( lambda c : c[0] )
cabin = pd.get_dummies( cabin['Cabin'] , prefix = 'Cabin' )
cabin.head()
| Cabin_A | Cabin_B | Cabin_C | Cabin_D | Cabin_E | Cabin_F | Cabin_G | Cabin_T | Cabin_U | |
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 2 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 3 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 4 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Nem todos os dados contidos no dataset são úteis ou relevantes. Abaixo foram selecionados apenas os dados que se mostraram influenciar de alguma forma na sobrevivência dos passageiros. Ex: Número de irmão (SibSp) e número de filhos (parch) não mostraram grande influência e foram removidos.
full_X = pd.concat( [ imputed , embarked , pclass , sex, cabin ] , axis=1 )
full_X.tail()
| Age | Fare | Embarked_C | Embarked_Q | Embarked_S | Pclass_1 | Pclass_2 | Pclass_3 | Sex | Cabin_A | Cabin_B | Cabin_C | Cabin_D | Cabin_E | Cabin_F | Cabin_G | Cabin_T | Cabin_U | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1304 | 29.881138 | 8.0500 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1305 | 39.000000 | 108.9000 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1306 | 38.500000 | 7.2500 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1307 | 29.881138 | 8.0500 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
| 1308 | 29.881138 | 22.3583 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 |
Alguns classificadores (especialmente redes neurais) tendem a convergirem mais rapidamente se os dados estiverem normalizados. Por esse motivo, abaixo os dados numéricos contínuos (Age e Fare) são normalizados.
from sklearn.model_selection import train_test_split
full_X_norm = full_X.apply(lambda x: (x - np.mean(x)) / (np.max(x) - np.min(x)))
full_X['Age'] = full_X_norm['Age']
full_X['Fare'] = full_X_norm['Fare']
#full_X['SibSp'] = full_X_norm['SibSp']
#full_X['Parch'] = full_X_norm['Parch']
Após a normalização do dataset completo é necessário separá-lo novamente entre treinamento e testes.
# Create all datasets that are necessary to train, validate and test models
train_valid_X = full_X[ 0:891 ]
train_valid_y = titanic.Survived
test_X = full_X[ 891: ]
train_X , valid_X , train_y , valid_y = train_test_split( train_valid_X , train_valid_y , train_size = .7 )
Classificação
O problema de predição de sobreviventes pode ser expressado como um problema de classificação onde cada exemplo deve ser classificado entre sobrevivente ou não. Abaixo foram realizados alguns testes com diferentes classificadores.
SVM (Support Vector Machine)
Abaixo são realizados o treinamento de máquinas de vetor de suporte (com kernel linear e rbf). O código realiza o treinamento de algumas SVMs utilizando diversos parâmetros informados na variável tuned_parameters. Após o treinamento é selecionado o conjunto de parâmetros que obteve a melhor acurácia.
import warnings
warnings.filterwarnings('ignore')
from __future__ import print_function
from sklearn.svm import SVC, LinearSVC
from sklearn.metrics import classification_report
from sklearn.model_selection import GridSearchCV
tuned_parameters = [{'kernel': ['rbf'], 'gamma': [1e-2, 1e-3, 1e-4, 1e-5],
'C': [1, 10, 100, 1000]},
{'kernel': ['linear'], 'C': [1, 10, 100, 1000]}]
scores = ['precision', 'recall']
for score in scores:
model = GridSearchCV(SVC(C=1), tuned_parameters, cv=5,
scoring='%s_macro' % score)
model.fit(train_X , train_y)
# Score the model
print (model.score( train_X , train_y ) , model.score( valid_X , valid_y ))
print("Best parameters set found on development set:")
print()
print(model.best_params_)
print()
print("Grid scores on development set:")
print()
means = model.cv_results_['mean_test_score']
stds = model.cv_results_['std_test_score']
for mean, std, params in zip(means, stds, model.cv_results_['params']):
print("%0.3f (+/-%0.03f) for %r"
% (mean, std * 2, params))
print()
print("Detailed classification report:")
print()
print("The model is trained on the full development set.")
print("The scores are computed on the full evaluation set.")
print()
y_true, y_pred = valid_y, model.predict(valid_X)
print(classification_report(y_true, y_pred))
print()
0.8378125 0.841176470588
Best parameters set found on development set:
{'C': 1000, 'gamma': 0.01, 'kernel': 'rbf'}
Grid scores on development set:
0.778 (+/-0.073) for {'C': 1, 'gamma': 0.01, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 1, 'gamma': 0.001, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 1, 'gamma': 0.0001, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 1, 'gamma': 1e-05, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 10, 'gamma': 0.01, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 10, 'gamma': 0.0001, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 10, 'gamma': 1e-05, 'kernel': 'rbf'}
0.770 (+/-0.081) for {'C': 100, 'gamma': 0.01, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 100, 'gamma': 0.0001, 'kernel': 'rbf'}
0.306 (+/-0.002) for {'C': 100, 'gamma': 1e-05, 'kernel': 'rbf'}
0.818 (+/-0.067) for {'C': 1000, 'gamma': 0.01, 'kernel': 'rbf'}
0.770 (+/-0.081) for {'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 1000, 'gamma': 0.0001, 'kernel': 'rbf'}
0.778 (+/-0.073) for {'C': 1000, 'gamma': 1e-05, 'kernel': 'rbf'}
0.770 (+/-0.081) for {'C': 1, 'kernel': 'linear'}
0.770 (+/-0.081) for {'C': 10, 'kernel': 'linear'}
0.770 (+/-0.081) for {'C': 100, 'kernel': 'linear'}
0.770 (+/-0.081) for {'C': 1000, 'kernel': 'linear'}
Detailed classification report:
The model is trained on the full development set.
The scores are computed on the full evaluation set.
precision recall f1-score support
0.0 0.80 0.95 0.87 168
1.0 0.88 0.60 0.71 100
avg / total 0.83 0.82 0.81 268
0.774956074706 0.785714285714
Best parameters set found on development set:
{'C': 1, 'kernel': 'linear'}
Grid scores on development set:
0.762 (+/-0.072) for {'C': 1, 'gamma': 0.01, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 1, 'gamma': 0.001, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 1, 'gamma': 0.0001, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 1, 'gamma': 1e-05, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 10, 'gamma': 0.01, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 10, 'gamma': 0.001, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 10, 'gamma': 0.0001, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 10, 'gamma': 1e-05, 'kernel': 'rbf'}
0.762 (+/-0.079) for {'C': 100, 'gamma': 0.01, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 100, 'gamma': 0.001, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 100, 'gamma': 0.0001, 'kernel': 'rbf'}
0.500 (+/-0.000) for {'C': 100, 'gamma': 1e-05, 'kernel': 'rbf'}
0.761 (+/-0.053) for {'C': 1000, 'gamma': 0.01, 'kernel': 'rbf'}
0.762 (+/-0.079) for {'C': 1000, 'gamma': 0.001, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 1000, 'gamma': 0.0001, 'kernel': 'rbf'}
0.762 (+/-0.072) for {'C': 1000, 'gamma': 1e-05, 'kernel': 'rbf'}
0.763 (+/-0.078) for {'C': 1, 'kernel': 'linear'}
0.762 (+/-0.079) for {'C': 10, 'kernel': 'linear'}
0.762 (+/-0.079) for {'C': 100, 'kernel': 'linear'}
0.762 (+/-0.079) for {'C': 1000, 'kernel': 'linear'}
Detailed classification report:
The model is trained on the full development set.
The scores are computed on the full evaluation set.
precision recall f1-score support
0.0 0.85 0.82 0.83 168
1.0 0.71 0.75 0.73 100
avg / total 0.80 0.79 0.80 268
Multi-layer Perception - MLP (Scikit Learn)
Treinamento utilizando o classificador MLP com algoritmo Stochastic Gradient Descent (SGD) e 6 neurônios na camada oculta.
from sklearn.neural_network import MLPClassifier
model = MLPClassifier(solver='sgd', alpha=1e-5, hidden_layer_sizes=(6, 2), random_state=1)
model.fit( train_X , train_y )
# Score the model
print ("Train: ", model.score( train_X , train_y ))
print ("Test:", model.score( valid_X , valid_y ))
Train: 0.781701444623
Test: 0.798507462687
Árvore de Decisão (Decision Tree)
from sklearn import tree
model = tree.DecisionTreeClassifier()
model.fit(train_X , train_y)
print ("Train: ", model.score( train_X , train_y ))
print ("Test:", model.score( valid_X , valid_y ))
Train: 0.987158908507
Test: 0.813432835821
### Adaboost
from sklearn.ensemble import AdaBoostClassifier
model = AdaBoostClassifier(n_estimators=50)
model.fit(train_X , train_y)
print ("Train: ", model.score( train_X , train_y ))
print ("Test:", model.score( valid_X , valid_y ))
Train: 0.84911717496
Test: 0.832089552239
### Gradient Boosting
from sklearn.ensemble import GradientBoostingClassifier
model = GradientBoostingClassifier(n_estimators=100, learning_rate=1.0, max_depth=1, random_state=0)
model.fit(train_X , train_y)
print ("Train: ", model.score( train_X , train_y ))
print ("Test:", model.score( valid_X , valid_y ))
Train: 0.873194221509
Test: 0.820895522388
Gaussian Naive Bayes
from sklearn.naive_bayes import GaussianNB
model = GaussianNB()
model.fit(train_X , train_y)
print ("Train: ", model.score( train_X , train_y ))
print ("Test:", model.score( valid_X , valid_y ))
Train: 0.711075441413
Test: 0.716417910448
Para utilização com o Keras é necessário converter os dados de Pandas para Numpy
from keras.utils.np_utils import to_categorical
t_X = train_X.as_matrix()
t_y = train_y.as_matrix()
#t_y = to_categorical(t_y)
v_X = valid_X.as_matrix()
v_y = valid_y.as_matrix()
#v_y = to_categorical(v_y)
test_X_m = test_X.as_matrix()
print(test_X_m)
Using TensorFlow backend.
[[ 0.05785873 -0.04970687 0. ..., 0. 0. 1. ]
[ 0.21444147 -0.05132536 0. ..., 0. 0. 1. ]
[ 0.40234075 -0.04607971 0. ..., 0. 0. 1. ]
...,
[ 0.10796521 -0.05083739 0. ..., 0. 0. 1. ]
[ 0. -0.04927589 0. ..., 0. 0. 1. ]
[ 0. -0.02134795 1. ..., 0. 0. 1. ]]
Multi-layer Perceptron (Keras)
Abaixo é criado um classificador MLP com 20 neurônios na camada intermediária e dropout de 50%. Foi utilizada a função de ativação sigmoid, a função de loss mean squared error e o otimizador RMSProp. O treinamento é realizado por 200 épocas com batch size de 64.
from keras.models import Sequential
from keras.layers import Dense, Dropout, Activation
from keras.optimizers import SGD
model = Sequential()
model.add(Dense(20, input_dim=t_X.shape[1], activation='sigmoid'))
model.add(Dropout(0.5))
model.add(Dense(1, activation='sigmoid'))
model.compile(loss='mse', optimizer='rmsprop', metrics=['accuracy'])
print(model.summary())
____________________________________________________________________________________________________
Layer (type) Output Shape Param # Connected to
====================================================================================================
dense_1 (Dense) (None, 20) 380 dense_input_1[0][0]
____________________________________________________________________________________________________
dropout_1 (Dropout) (None, 20) 0 dense_1[0][0]
____________________________________________________________________________________________________
dense_2 (Dense) (None, 1) 21 dropout_1[0][0]
====================================================================================================
Total params: 401
Trainable params: 401
Non-trainable params: 0
____________________________________________________________________________________________________
None
hist = model.fit(t_X, t_y,
batch_size=64,
nb_epoch=200,
verbose=False)
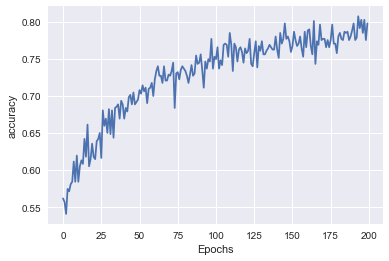
O gráfico de acurácia em relação a época de treinamento mostra a evolução em relação ao tempo.
plot_line(hist.history['acc'], 'accuracy')
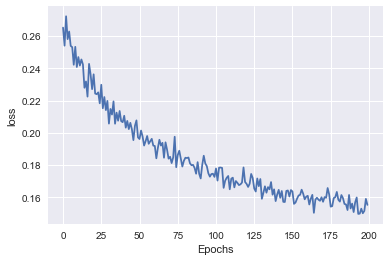
O gráfico de erro (loss) mostra como o erro é reduzido a cada etapa de treinamento. Funciona como um "debug" para visualizar se o treinamento está ocorrendo corretamente. Se o erro não mudar em relação a época é sinal que existe algo errado com o classificador ou seus parâmetros.
plot_line(hist.history['loss'], 'loss')
loss, accuracy = model.evaluate(v_X, v_y)
print("Loss: ", loss)
print("Accuracy: ", accuracy)
32/268 [==>...........................] - ETA: 0sLoss: 0.13912824975
Accuracy: 0.828358208955
Deployment
O código abaixo realiza a predição de cada um dos exemplos de teste e armazena em um arquivo em formado aceito pelo Kaggle.
t_X = test_X.as_matrix()
test_Y = model.predict( t_X )
test_Y = test_Y.flatten().round().astype(int)
passenger_id = full[891:].PassengerId
test = pd.DataFrame( { 'PassengerId': passenger_id , 'Survived': test_Y } )
test.shape
test.head()
test.to_csv( 'titanic_pred.csv' , index = False )